Multiobjective Bilevel Optimization: A Survey of the State-of-the-Art
Jesús-Adolfo Mejía-de-Dios 8 min readOptimization makes processes, systems, or products more efficient, reliable, and with better outcomes. A popular topic on optimization today is Multi-Objective Bilevel Optimization (MOBO). In MOBO, an upper-level problem is constrained by the solution of a lower-level one. The problem at each level can include multiple conflicting objective functions and its own constraints. This survey aims to study the solution approaches proposed to solve MOBO problems, including exact methods and approximate techniques such as meta-heuristics. This work explores classical literature to investigate why most classical methods, theories, and algorithms focus on linear and some convex MOBO problems to solve the optimistic MOBO. Moreover, we study and propose a taxonomy of meta-heuristic-based frameworks for solving some MOBO instances, highlighting the pros and cons of five main approaches.
This post is based on the paper:
Jesús-Adolfo Mejía-de-Dios, Alejandro Rodríguez-Molina, Efrén Mezura-Montes, Multiobjective Bilevel Optimization: A Survey of the State-of-the-Art in IEEE Transactions on Systems, Man, and Cybernetics: Systems, 1-13, 2023.
Introduction
In some engineering problems, the solutions should satisfy a single criterion, e.g., the design of a robot that increases its dexterity during surgery, the scheduling that increases furnace productivity in an annealing plant, or the prediction of market values that ensures the best investment.
However, there are cases in which these solutions must meet two or three conflicting objectives, i.e., one requirement cannot be fully satisfied without affecting compliance with the other. This type is known as a multi-objective optimization problem (MOP).
Within this area, one can find problems in which opposing criteria are simultaneously optimized, such as reducing power consumption and execution time of computing tasks in the cloud; lowering manufacturing costs and environmental impact while increasing product quality in a pharmaceutical supply chain; or minimizing costs in the construction of a gas procurement plant with lower environmental impact.
The solution to this type of problem is a set of alternatives that represent unbeatable trade-offs between the criteria. In this sense, Decision-Making (DM) is necessary to select the most suitable option for practical application.
Multi-Objective Bilevel Optimization
Multi-Objective Bilevel Optimization (MOBO) and Semi-Vectorial Bilevel Optimization (SVBO) are briefly described in this section. A MOBO problem is a bilevel optimization problem involving one or two multi-objective optimization tasks in a hierarchical structure and can be defined as follows.
Consider the following functions $F : X \times Y \to \mathbb{R}^M $, $f : X \times Y \to \mathbb{R}^m$ with $M,m$ positive integers such that $M\geq 2$ and $m \geq 1$. Then, the following problem defines a MOBO problem:
Minimize (UL)
\begin{equation}
F(\vec{x}, \vec{y}) = (
F_1(\vec{x}, \vec{y}), F_2(\vec{x}, \vec{y}) , \ldots , F_M(\vec{x}, \vec{y})
)
, \
\vec{x} \in X
\end{equation}
subject to:
\begin{align}
\vec{y} &\in \argmin_{\vec{y}\in Y}
\left\{
\begin{matrix}
f( \vec{x}, \vec{y} )
= (f_1(\vec{x}, \vec{y}), \ldots , f_m(\vec{x}, \vec{y}))
: \\
g_j( \vec{x}, \vec{y} ) \leq 0, \ j=1,2,\ldots,J
\end{matrix}
\right\}
\\
& G_k(\vec{x}, \vec{y}) \leq 0, \ k=1,2,\ldots,K;
\end{align}
where $G_k, g_j: X \times Y \to \mathbb{R}$, represent the upper and LL constraints ($1 \leq k \leq K$, $1\leq j \leq J$), respectively.
A SVBO problem contains a single-objective function $F:X\times Y \to \mathbb{R}$, but the LL is a MOP $f:X\times Y \to \mathbb{R}^m$ as in above formulation with $M = 1$ and $m \geq 2$ (see [1]). Note that, other works define MOBO as in the above formulation but considering $M \geq 2$ or $m \geq 2$, implying that SVBO is a special case of MOBO in other definitions.
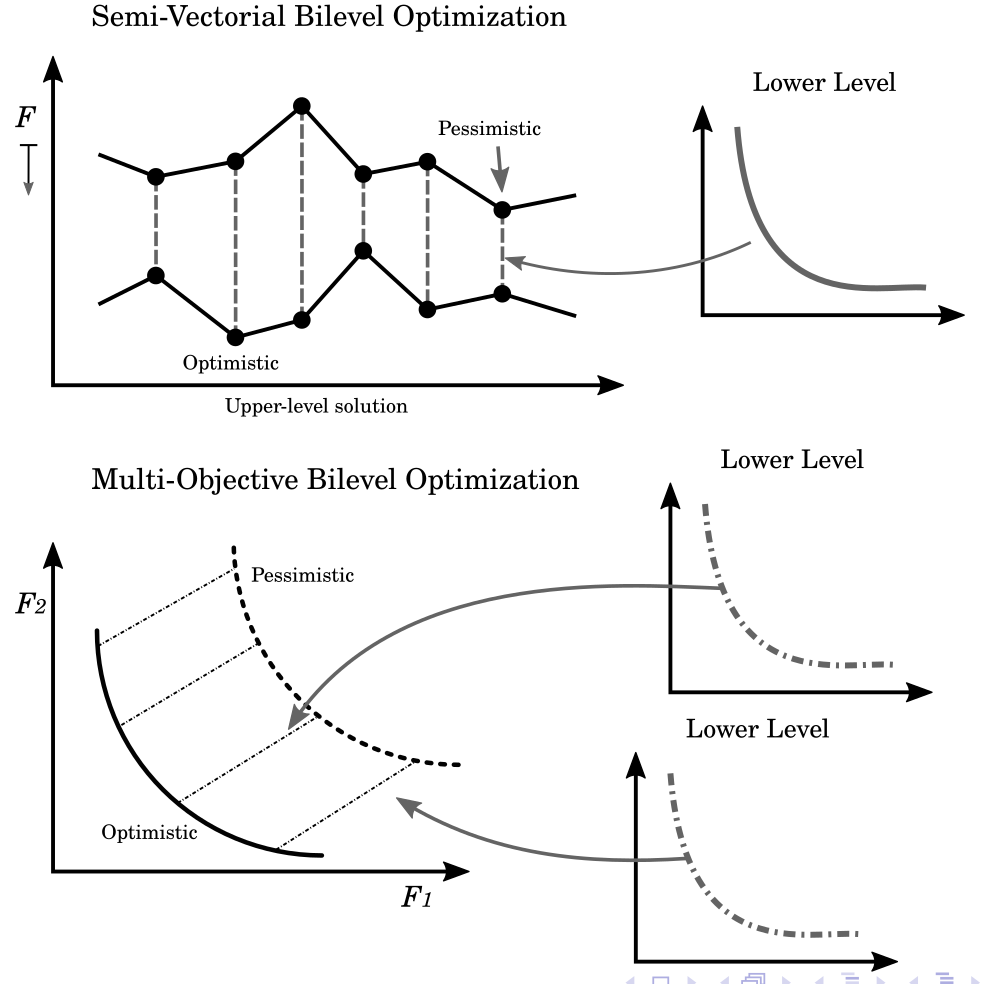
The goal of a bilevel optimization problem is governed by the UL problem, which is the optimization problem to be solved subject to the inequality constraints, and also to the optimality of the LL problem. Thus, in practice, the aim of an SVBO problem is to find an optimal feasible solution for the single-objective problem defined at the UL.
On the other hand, the aim of a multiobjective bilevel optimization problem is similar to that of single-level MOPs, i.e., it is desirable (in practice) to find a set of feasible solutions distributed along the Pareto-optimal front given by the UL multi-objective problem, while satisfying the lower-level optimality. Moreover, if both levels contain single-objective problems, it is not a multiobjective bilevel model, but a single-objective bilevel one.
The feasibility notion in multiobjective bilevel optimization is different from single-objective bilevel optimization, since the leader can require the follower to make decisions based on a set of Pareto-optimal solutions when $m > 1$.
Classical Solution Approaches
Different studies have been carried out to address the optimistic and pessimistic positions in MOBO and SVBO. However, most works are devoted to solving the optimistic case, since the pessimistic position is, in general, less tractable than the optimistic one.
This section is used to review classical algorithms proposed for MOBO. Because MOPs are usually difficult to solve, most works that use classical optimization techniques suppose that the problems are well-characterized, and their mathematical properties satisfy assumptions. The same is true when exact methods for MOP are extended to handle MOBO problems. Common assumptions in MOBO are those related to continuity, differentiability, convexity, and linearity of constraints and objective functions.
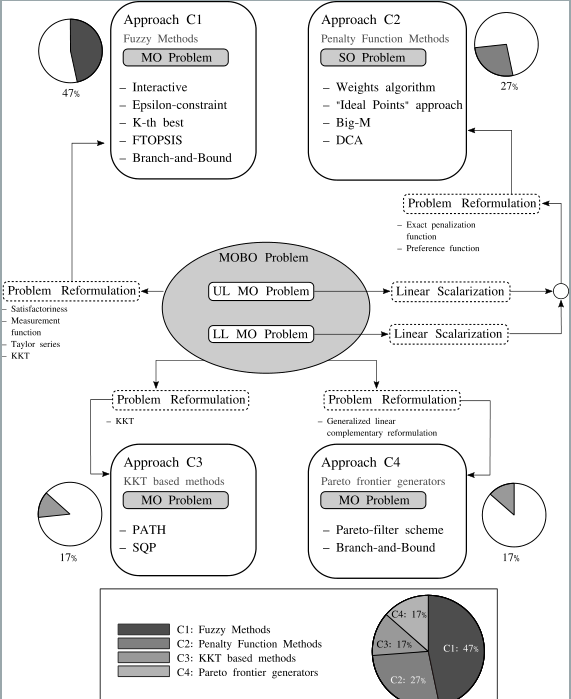
- Approach C1: Fuzzy Methods: A fuzzy method is referred to as (a method) using fuzzy logic concepts to find efficient solutions to (fuzzy) MOBO problems
- Approach C2: Penalty Function Methods: Classical methods that use a penalty function approach are focused on performing a single-level reduction by adding the LL functions to the UL as a penalization term. Thus, each penalization strategy is based on different mathematical concepts for transforming the bilevel problem into a tractable MOP.
- Approach C3: Methods based on Karush-Kuhn-Tucker Conditions: The Karush-Kuhn-Tucker (KKT) conditions extend the Lagrangian multipliers method for transforming constrained optimization problems into an equivalent and more tractable formulation. In the bilevel optimization context, KKT conditions are commonly used for single-level reduction when the LL problem contains objective functions and constraints that are convex and smooth enough.
- Approach C4: Pareto Frontier Generators: Most classical approaches have been proposed to approximate a solution in the Pareto optimal set by using either a priori preferences or interactive methods. However, some proposals are trying to approximate solutions along the Pareto optimal front, and in this literature review, they are referred to as Pareto Frontier Generators.
Metaheuristic Approaches
After deep research in the MOBO specialized literature, five Metaheuristic (MH) approaches are identified and illustrated in figure below.
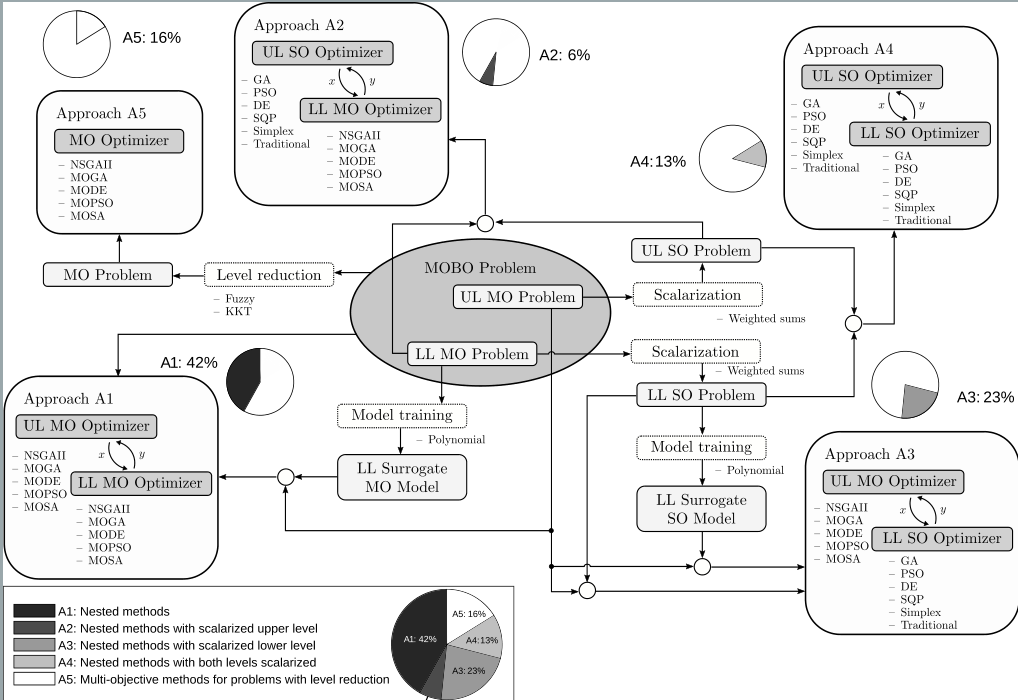
- A1: Nested methods: In this approach, two multi-objective methods are nested to solve the MOBO model.
- A2: Nested methods with scalarized UL: In the A2 approach, the UL can be naturally a single-objective problem or a scalarized multi-objective one. At the same time, there is a MOP at the LL. Only a couple of works are found here.
- A3: Nested methods with scalarized LL: In A3, the LL originally has either a single-objective problem or a scalarized multi-objective one, while there is a MOP at the UL. A3 is less expensive than A1 and A2 since there is no subset of LL alternatives for each UL solution, but only a single one.
- A4: Nested methods with both levels scalarized: In this case, the problems at both levels are scalarized if they are not initially given in a single-objective form. Afterwards, two single-objective methods are nested to solve the UL and LL problems.
- A5: Multi-objective methods for problems with level reduction: In A5, the MOBO problem has specific conditions that allow the LL to be embedded in the UL. Therefore, a multi-objective metaheuristic can solve the MOBO model transformed into a multi-objective single-level problem.
Note: When a LL metaheuristic solves the LL, different issues emerge due to the inaccurate nature of such a LL optimizer. In general, a LL metaheuristic provides infeasible solutions to the UL. It can be recommended, as much as possible, to use a local search via some applicable exact algorithms to mitigate this issue. Other mechanisms should be proposed even when uncertainty is present. Also, when the LL Pareto front is accurate enough but with a low diversity rate, UL fronts between the optimistic and pessimistic front can be generated. More work is required to assess this issue.
Conclusions
This work presented an in-depth study of the state-of-the-art on multiobjective bi-level optimization based on classical methods and metaheuristic techniques, analyzing the available solution methods and applications. A general overview of this type of optimization was given during the survey, while the shortcomings and the most notable aspects of both solution approaches were emphasized.
On the classical approach, a significant amount of works can address problems with predefined characteristics, such as convexity, linearity, and differentiability. Nevertheless, there is a lack of theoretical evidence on how these methods can solve problems with a wider variety of characteristics.
Regarding metaheuristics, the amount of work is limited and has focused on solving problems similar to those of the classical methods. Still, there is an evolution of this approach toward solving more complex problems related to real-world applications. In this case, it is necessary to test new operating schemes based on those effective for other types of optimization problems and develop new metrics, decision-makers, and constraint handlers.
Citation
Please cite our paper:
@ARTICLE{mobo-survey-2023,
author={Mejía-de-Dios, Jesús-Adolfo and Rodríguez-Molina, Alejandro and Mezura-Montes, Efrén},
journal={IEEE Transactions on Systems, Man, and Cybernetics: Systems},
title={Multiobjective Bilevel Optimization: A Survey of the State-of-the-Art},
year={2023},
volume={},
number={},
pages={1-13},
doi={10.1109/TSMC.2023.3271125}
}
