Search
for information on this portal
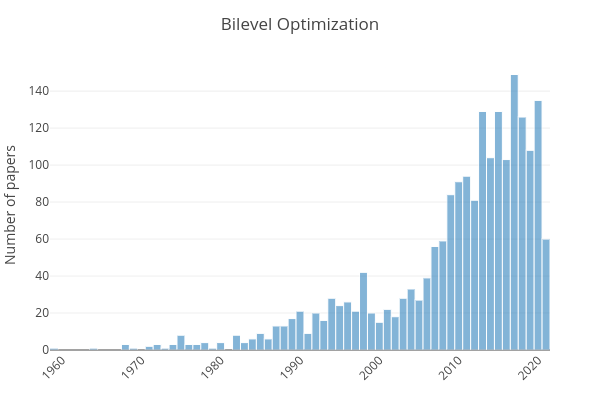
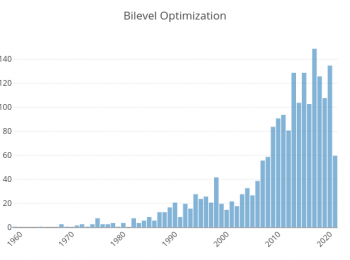
Bilevel Optimization
Optimization refers to the process of finding the best possible solution among a set of alternatives for a specific problem or objective. It involves maximizing or minimizing an objective function.
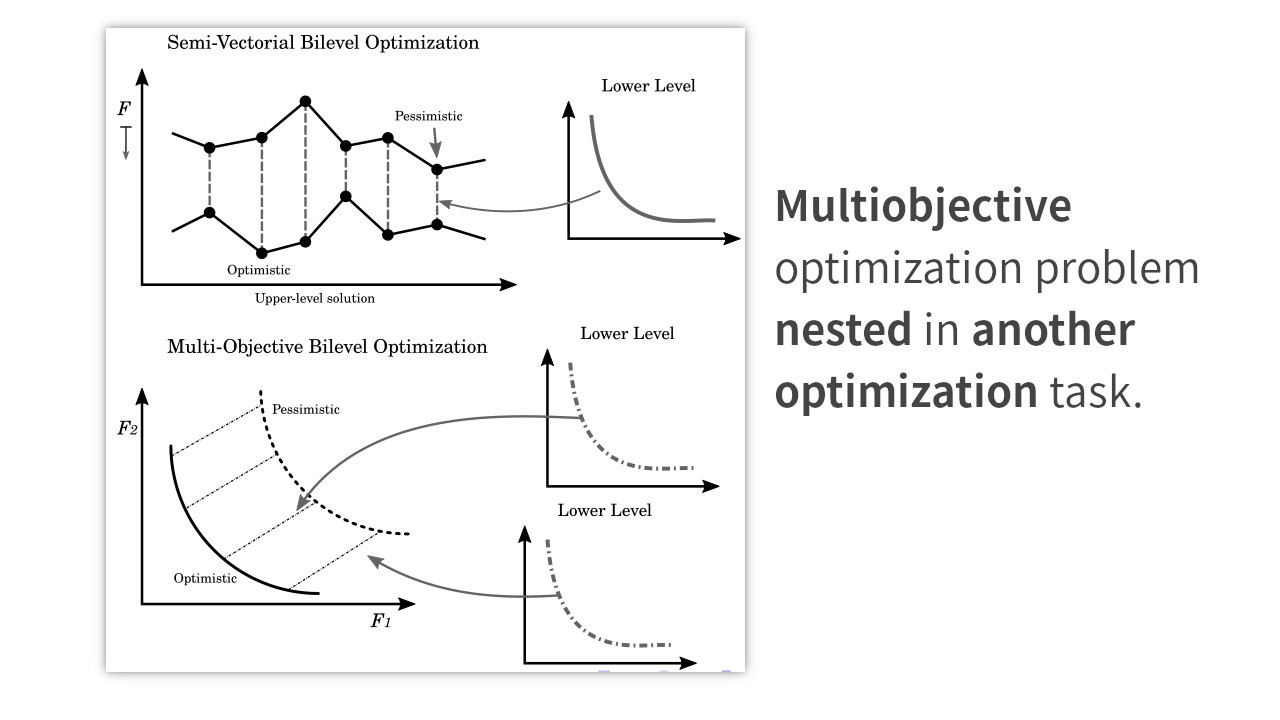
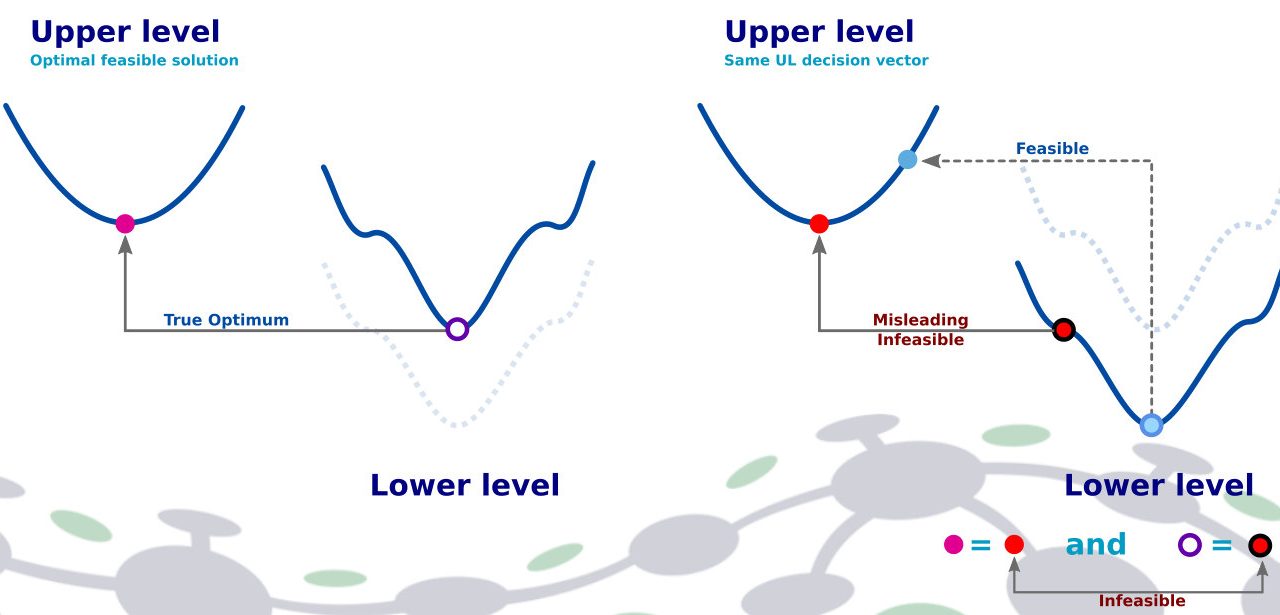
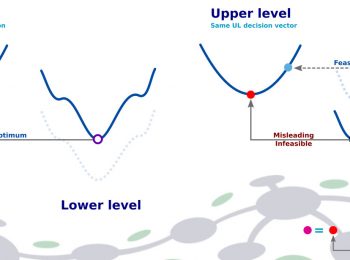
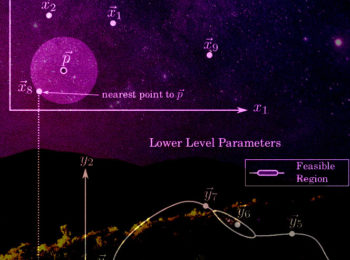
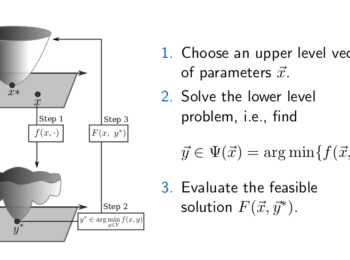
Bilevel optimization is a type of optimization problem that involves an optimization problem nested within another.
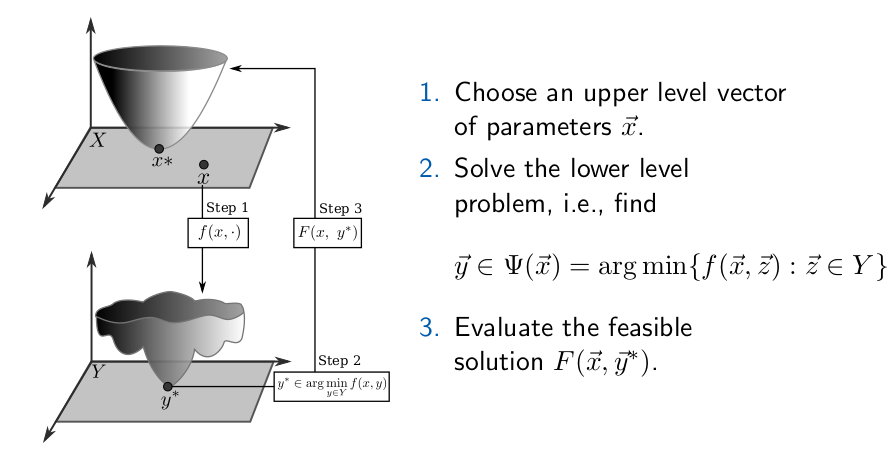
In this scenario, the upper-level problem, also known as the leader problem, aims to optimize a global objective function while considering the solutions of the lower-level problem, known as the follower problem.
See this tutorial to learn more or explore our content.
Optimization
Resources for Optimization topics
Algorithms
Available software containing methods for Bilevel Optimization
Tutorials
Tutorials on Bilevel Optimization and more stuff related to.
Information
Research Groups
Research groups dedicated to solving bi-level optimization problems.